
Une malheureuse réalité lorsqu'on essaie de représenter des nombres réels continus dans un espace fixe (par exemple avec un nombre limité de bits) est que cela s'accompagne d'une perte inévitable de précision et d'exactitude. Bien que les normes arithmétiques à virgule flottante – comme la norme IEEE 754 couramment utilisée – cherchent à minimiser cette erreur, il est inévitable qu'une perte de précision se produise sur la plage d'une variable à virgule flottante. C'est quoi [exozy] le démontre, en montrant à quel point l'erreur peut atteindre lors de l'exécution d'une simple division de l'exponentielle d'une valeur d'entrée par la valeur d'origine. Cela entraîne une erreur étonnante de plus de 10 %, ce qui soulève la question de savoir comment résoudre au mieux ce problème.
Évidemment, si vous en avez la possibilité, vous pouvez simplement augmenter la précision de la variable à virgule flottante, de 32 bits à 64 ou même 256 bits, mais cela ne vous mène pas loin. La solution qui [exozy] montre ici implique d'utiliser un calcul redondant en inversant le résultat de eX. Dans une démonstration utilisant du code Python (qui utilise la double précision IEEE 754 en interne), cela élimine presque l'erreur. En plus de prouver que l’arithmétique à virgule flottante est maudite, cela soulève également la question de savoir pourquoi cela fonctionne.
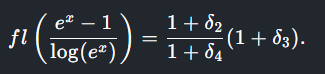
Pour l'explication, une compréhension de base du calcul est plutôt utile, car [exozy] regarde la fonction d'origine (f(x)) et la version avec le logarithme ajouté (g(x)). Avec une hypothèse faite sur l'erreur résultant de chaque opération arithmétique (δ), les deux fonctions peuvent être analysées, en ajoutant un 1 + δ hypothèse faisant suite à chacune de ces opérations et en les simplifiant autant que possible. Pour f(x) il devient clair que c'est le dénominateur qui est la cause de l'erreur, mais il faut regarder g(x) pour donner un sens à ce qui change.
Intuitivement, log(ex) aide car il annule d'une manière ou d'une autre l'erreur dans ex, mais ce qui se passe réellement, c'est qu'avec les petites entrées utilisées pour x (g(1e-9), g(1e-12) et g(1e-15)) les approximations aboutissent à la décomposition simplifiée présentée ici (fl()). Avec un plus grand x, les développements en série de Taylor utilisés dans l'analyse ne s'appliquent plus. Ce qui semblait être une solution ne fonctionne plus, et nous nous retrouvons avec la dure réalité que représenter des nombres réels dans un espace fixe sera à jamais le domaine des larmes et des rêves brisés.




































